A una de nosotras le toco hablar sobre las curvas cónicas así que les explicaremos brevemente que son:
Curvas:
Una curva es una linea (real o imaginaria) que se aparta de la dirección recta sin formar ángulos. Esto quiere decir que su dirección varía de manera paulatina y constante.
Curvas conicas:
Dependiendo de la inclinación del plano respecto al eje podemos obtener las siguientes cuatro formas:
Si consideramos el eje vertical, obtenemos:
Circunferencia.- Se obtiene al cortar el cono por un plano horizontal.
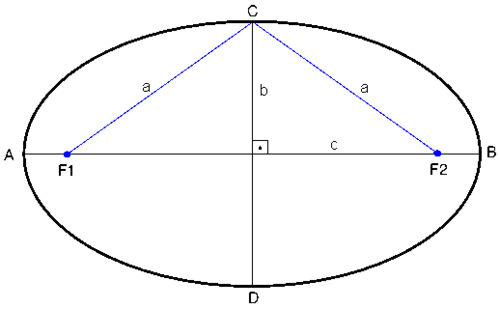
Elipse.- Se obtiene al cortar el cono por un plano oblicuo, de inclinación menor que la generatriz
Parábola.- Se obtiene al cortar el cono por un plano paralelo a la generatriz
Hipérbola.- Se obtiene al cortar el cono por un plano oblicuo de mayor inclinación que la generatriz. Esta curva tiene dos ramas.
Esto fue todo lo hablado en la primera exposición
Mi compañera Isabella hablo sobre la parábola, les explicaremos que es:
Parábola:
Es una curva cónica, abierta, plana y de una sola rama.
Los elementos esenciales de la parábola son:
- El foco
- La directriz
- El eje
- El vértice
Los puntos de la parábola cumplen que son equidistantes de la directriz y del foco.
Construcción de la parábola - Por puntos
- Por haces proyectivos
- Por envolventes